The linear regression function is in the form
![]() (1)
(1)
where ![]() is the muscle activity (regressand) to be reconstructed and
is the muscle activity (regressand) to be reconstructed and
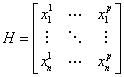
is the design matrix with the time series of a set of p voxels from the selected ROI in the 'regression set'. The parameters ![]() will be computed to realize the best mapping of the voxels to the muscle activity while making the function sparse.
will be computed to realize the best mapping of the voxels to the muscle activity while making the function sparse. ![]() is the noise for n brain scans recorded in an experiment.
is the noise for n brain scans recorded in an experiment.
To favour a sparse representation, a Laplacian prior is chosen for β such that
![]()
where ![]() and α is the parameter of this density, then the maximum a posteriori estimate of β is given by
and α is the parameter of this density, then the maximum a posteriori estimate of β is given by
![]() (2)
(2)
The term with the Euclidean norm || ||2 expresses the least-square approximation of the regress and, while the term || ||1is to produce a sparse representation. The || ||1norm, corresponding to the absolute value, has a larger gradient than the || ||2 norm in the vicinity of the minimum and thus should converge fast to zero, i.e. to a sparse representation. This criterion was named as least absolute shrinkage and selection operator or LASSO (Tibshirani 1996).
The Laplacian prior is equivalent to a two level hierarchical Bayes model with zero mean Gaussian priors with independent exponentially distributed variances (Figueiredo 2003; Lange and Sinsheimer 1993). This allows us to use the expectation- maximization (EM) algorithm to implement the LASSO criterion (Osborne et al. 2000, Tibshirani 1996) in two steps:
and
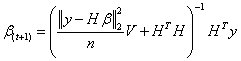
The parameter γ controlling the degree of sparseness of β may be eliminated using a Jeffreyfs non-informative hyper-prior.
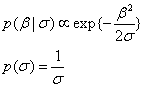 >
>This is equivalent to an automatic relevance determination (ARD) prior.
The EM steps may now be adjusted to get the following modified EM algorithm (Figueiredo 2003).
In our regression (4) and (5) are used to make β sparse, determined by the value of parameter σ. The optimal value of σ was determined by an adaptive process as explained in next section.
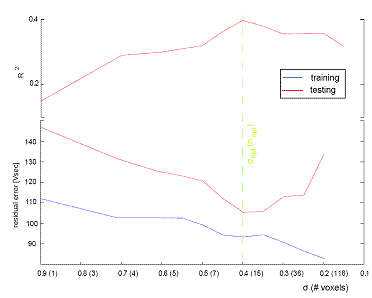
To achieve a good generalization of a model or mapping, it is necessary to control the complexity of the learnt function. If the function is too complex then it will reproduce unimportant details of the training set, thus over-fitting the training data. Such a function will fit the training data well but will be unable to predict a different test data well. Conversely, an overly simple function will not be able to capture the true mapping between the regressor and the regressand, thus under-fitting the training data. In our case the number of voxels chosen during training decides the ability of the model to generalize well. The typical behaviour of our data set is represented in (Fig. 1).
The regression algorithm has one free parameter (σ) to adjust the number of voxels used during training. We utilize over-fitting, detected by the performances on a representative portion of the test set, the selection
set, as a criterion to recursively select an optimal value of σ.
The EM algorithm loop starts with σ =1. The evaluated mapping vector σ is tested on the selection set and the coefficient of determination (R2) is evaluated. A binary search is used to determine the σ with minimal R2.
The performance has been quantified using the coefficient of determination 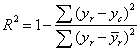 , where yr represents the muscle regressand value,
, where yr represents the muscle regressand value, ![]() r its average and yc the reconstructed value.
r its average and yc the reconstructed value.
- The regressand is the physical parameter that will be reconstructed/ decoded from the brain activity. We reconstructed the muscle EMG and thus used smoothed EMG activity as regressand.
- The regressand is re-sampled at the same frequency as the repetition time (TR) of the fMRI scan.
- This data is used in the training (yt), test (yr) and selection (ys)
- The brain images from the collected in different sessions should be realigned to the first scan of session 1 to ensure there was no displacement among scans from the different sessions.
- For each subject a region of interest (ROI), may be defined for reconstruction
- The voxel time series from the ROI (or entire brain) is extracted and band-pass filtered between 0.003 Hz (300 sec) and 0.2 Hz (5 sec) before the regression analysis. The low frequency cut-off value will remove any drift in the fMRI signal while the high cut-off of 0.2 Hz will reduce noise constrained by the frequency content of haemodynamic function (hrf). This preprocessed data was used as the regressor in the training (Xt), test (Xr) and selection (Xs) analysis.
sigma=1;% parameter to be calculated by over-fitting criterion
last=100;
% thresh=.05; % threshold of 5%
%while (abs(e(i-1)-e(i-2))>e(i-1)*thresh)
while (i<last)
V=diag(abs(<>beta(:,i)));
beta(:,i+1)=V*inv(sigma^2*diag(ones(k,1))+V*Xt'*Xt*V)*V*Xt'*yt;
%e(i)=sum(abs(yt-Xt*beta(:,i+1)));
i=i+1;
end;
%---------------------------------------------------
In the above code beta represents the m x t matrix of regression parameters of t iteration steps and m voxels. yt represents the n x 1 vector of regressand of n data points (scans) and Xt is the n x m matrix of voxel activity regressor.
In the first step the code starts with sigma=1. The 'while loop' may be run for a constant long time, e.g. 100 times. Conversely this may also be automated by checking for regression error. This may be done by commenting the current 'while' command and de-commenting the green lines. However, the convergence (thresh) may have to be tuned according to the noise in the data.yc=Xs*beta(:,last);% reconstruction in selection set
R2=1-sum((ys-yc).^2)/sum((ys-mean(ys)).^2); % coeff .of performance calculation
%-------------------------------------------------------------------------
- Check the value of R21 for a particular sigma (say σ1=1) using step 4 and step 5.
- Change the sigma, (say σ2=0.1) and calculate R22.
- If R22 > R21, then next choose s2 and try values around σ2.
- Check for sigma values, say σ3=0.5 and σ4=0.05 to get R23 and R24.
- If R23>R24 then choose σ3 and try values around σ3 like step IV else try values around σ4.
- Continue like in steps IV and V till convergence of R2 is achieved. This corresponds to the optimal σopt (sigma_opt) and gives the optimal beta (beta_opt) from step 4.
yc = Xr*beta_opt;
% reconstruction in test set
R2 = 1 - sum((yr-yc).^20)/sum((yr-mean(yr)).^2); % coeff .of performance of test
%-------------------------------------------------------------------------
A Matlab code for the above optimization procedure will be uploaded on this website in the near future. At present a population search algorithm is used for the purpose. This procedure may however take a long time and the recommended method is to optimize according to the steps given above.
The code is implemented for direct use in the program 'reconstruct.m' which takes data from 'data_sample.mat' and uses the function 'sp_regress.m'. 'data_sample.mat' contains muscle activity data from a wrist muscle as regressands (yt,ys,yr) recorded during fMRI. The brain activity from voxels from the motor cortex (area4, area6) make up the regressors (Xt,Xs,Xr). Function 'sp_regress.m' uses population search to optimize the parameter 'sigma'.
Sparse linear regression for reconstructing muscle activity from human cortical fMRI. Neuroimage, 42(4):1463-72, 2008
Adaptive sparseness for supervised learning. IEEE Trans. Pattern Analy. and Machine Intelligence, 25(9):1150-59, 2003.
Normal/Independent distributions and their applications in robust regression. J. Computational and Graphical Statistics 2: 175-198, 1993.
, A new approach to variable selection in least squares problems. IMA J. Numerical Analysis 20: 389-404, 2000.
Regression shrinkage and selection via the LASSO. J. Royal Statistical Soc. (B) 58: 267-288, 1996.
- sp_regress.m
- reconstruct.m
- data_sample.mat
- Sparse_reg.doc