Analysis and Control of Passive Running Robots

1. Objective

2. One-legged running robot

1) Model

Based on energy analysis, we proposed a novel stabilization controller for a planar one-legged robot shown in Fig. 1.

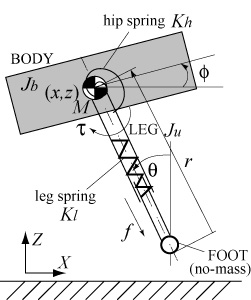
Fig. 1 One-legged passive running robot

2) Passive running gait

It is impossible to obtain periodic running gaits analytically. Therefore we developed numerical search algorithm using Newton-Raphson method, based on the exact nonlinear hybrid dynamics. It involves calculation of fundamental matrix solution of variational equation at each phase (including discrete jump phase). All the calculations are carried out in terms of Poincare Map .

Since the nontrivial passive running gaits are unstable period-one gaits (linealized Poincare Map has eigenvalues larger than unity), this robot cannot run without stabilizing controller. The instability increases as the forward speed does.

3) Controller

We proposed two kinds of controllers:

First, we derived a linear state feedback controller using only two control inputs that move the unstable poles to ZERO. This local feedback controller stabilizes running gaits, but its region of attraction is found to be very small, and large steady-state error remains.

Secondly, we derived a new simple controller. Instead of depending on some pre-calculated periodic solutions, or target (desired) dynamics, here we tried to utilize the natural dynamics of the original nonlinear hybrid system to generate (unknown) natural running gaits.

For this purpose, an energy-preserving control strategy has been proposed, in which the controller tries to minimize the dissipative energy as much as possible. The most important reason why we use this strategy is; if the system energy is preserved, the system is expected to generate natural periodic gaits, just as some class of Hamiltonian systems exhibit do.

This strategy led to a new touchdown controller at flight phase. Based on the energy dissipation analysis, the controller deadbeat the state to ensure the energy preservation at touchdown.

4) Simulation

Fig. 2 Quasi-periodic gait	Fig. 3 Quasi-periodic gait with disturbance

Simulation results shows that the robot can hop from wide set of initial conditions, and the generated running gaits are found to be quasi-periodic orbits, which can be seen in Hamiltonian system (Fig. 2). Since the controlled running gaits exist for every admissible energy level, they have some robustness against disturbances (Fig. 3).

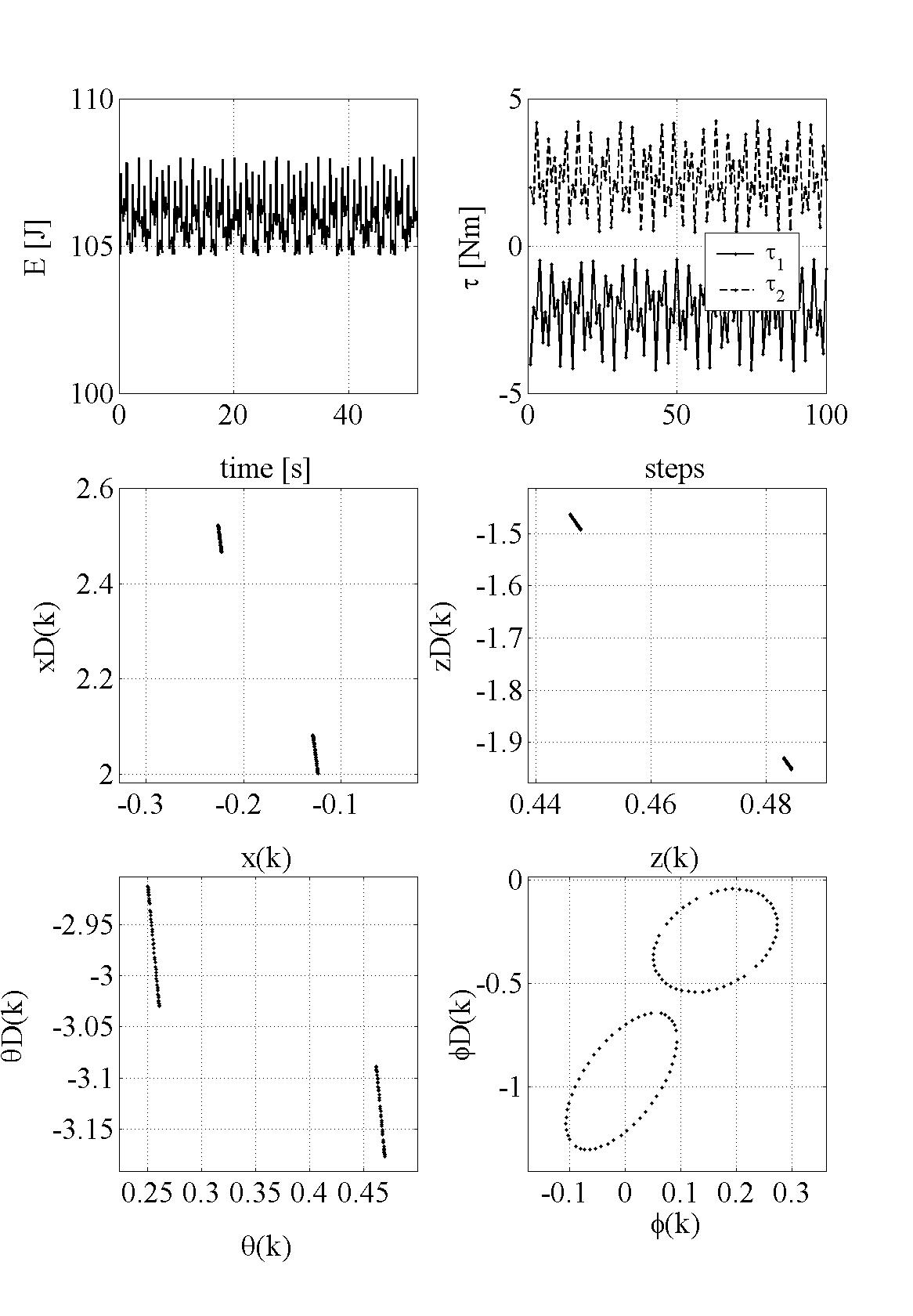
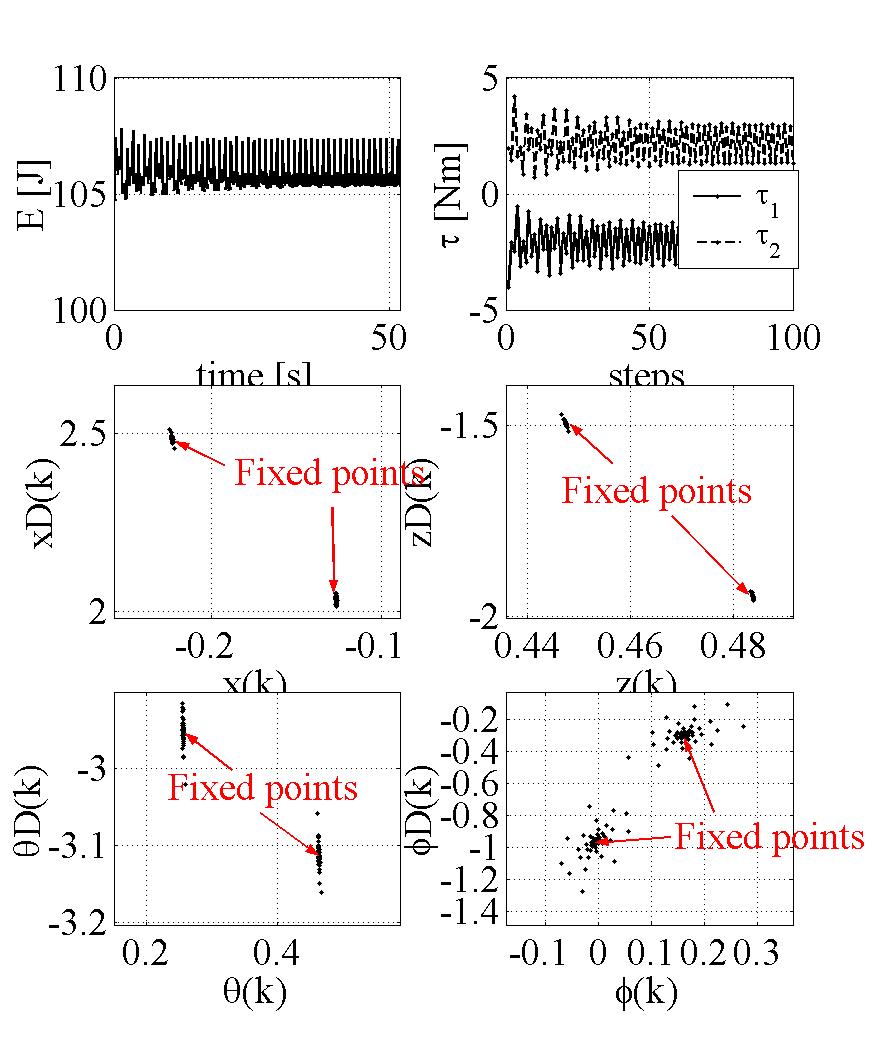
Fig. 4 Orbital stabilization to passive one-periodic gait	Fig. 5 Orbital stabilization to two-periodic gait

It is shown that simple adaptation laws, which is similar to delayed feedback controllers for chaotic systems, can asymptotically stabilize quasi-periodic gaits to the periodic ones having desired period for some cases (Fig. 4). In particular, for 1-periodic gait, the robot eventually hops without any control inputs (Fig. 5).

Animation

• Quasi-periodic running with disturbance [AVI 1,678K]

• High speed running at 5 m/s [AVI 923K]

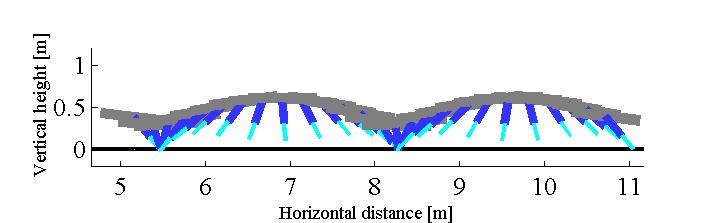
Fig. 6 Successive three-steps running at 5 m/s

3. Biped running robot

1) Model

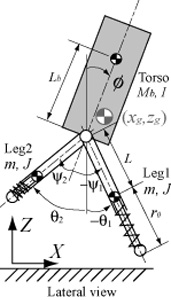
We consider a highly-nonlinear planar biped model having massive legs and torso (Fig. 7)

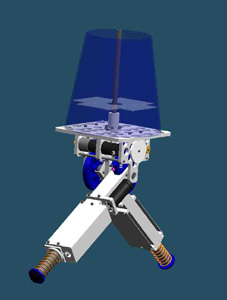Fig. 7 Planar biped running robot with torso	Fig. 8 Planar biped prototype

2) Controller

Unfortunately, complete passive running gaits cannot be found by numerical search algorithm. Nevertheless, we can stabilize this system. The controller of passive one-legged hopper is extended to the biped robots. Specifically, we derive dead-beat controller at flight phase based on the energy-preserving strategy to preserve mechanical energy at touchdown. Then, we combine this with a posture controller at stance-phase to obtain stable running gaits.

3) Simulation

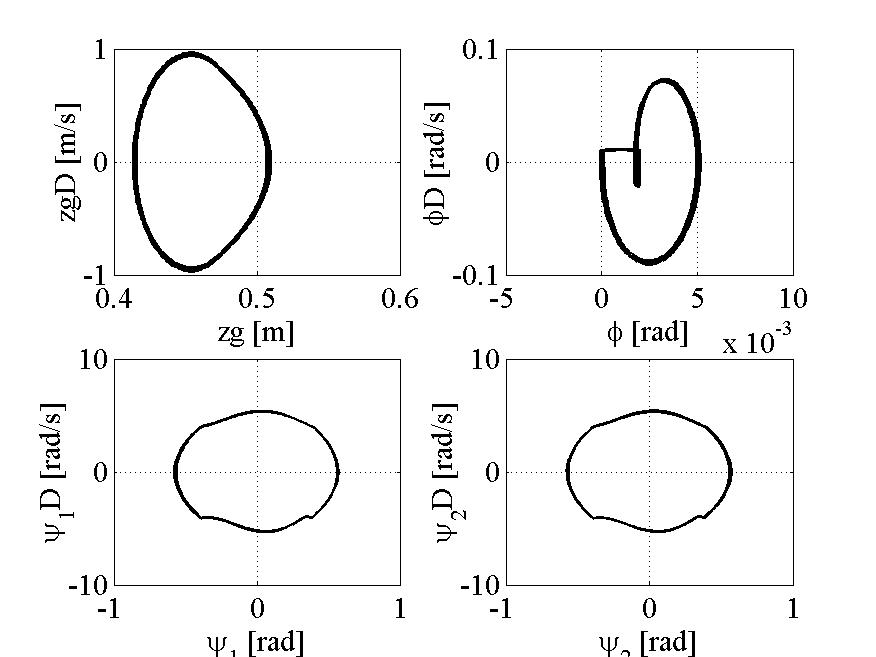
Fig. 9 Orbital stabilization to one-periodic gait

Although the running gaits seem to have symmetricity, there are a little asymmetricity in the torso motions, as recognized from the right top graph. This asymmetricity become more significant when the feedback gains of body attitude control is smaller. Without attitude control, the robot falls down after a few steps.

Animation

• Biped running at 4 m/s [AVI 633K]

• Biped running on a precise simulator [AVI 745K]

Rotational touchdown control of 3D biped prototype [AVI 222K]

4. Quadruped running robot

1) Model

The model of our robot is shown in Fig. 10. The legs are connected to the body through revolute joints. Each leg includes upper and lower sections, which are connected with a linear spring. The distance between the toe and hip changes because of the sliding motion between the lower and the upper section of the legs, so each leg has one linear passive degree of freedom.

The first research is to explore the properties of passive running, no control input assembles are configured in our profile. In replace, we set two springs in hips. This setting is expected to save the leg swinging energy. To summarize, each leg in our robot has two degree of freedom: a rotational one and a linear one and both of them are completely passive.

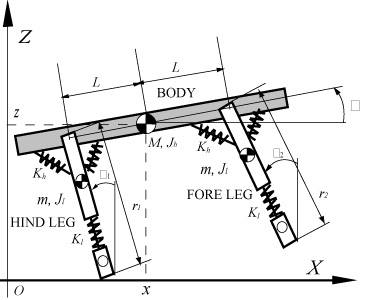
Fig. 10 Planar biped running robot with torso

2) Passive running gait

In a complete bounding cycle, a full stride of the robot can be divided in four different phases. These phases are:

• Back Leg Stance: the back legs support the robot while the front legs are in the air.
• Double Leg Stance: both legs are on the ground.
• Front Leg Stance: the front legs support the robot while the back legs are in the air.
• Double Leg Flight: both legs are in the air.

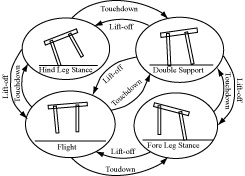
Fig. 11 Phase transition of planar quadruped running gait

Unlike the other related researches, we take the mass of the legs into account. Therefore our approach can capture not only the body's oscillatory pitch motion, but also reveal the properties of leg swinging. The non-zero mass assumption complexes the system by introducing impact and the formidable equations which can not be expressed well symbolically. To solve these problems, we apply Hybrid System Theory.

As we do not assume a specific running sequence for this algorithm, the propagation of the system follows no specific order. Only the gaits which tend to converge will exhibit a repetition of ordered phases.

3) Simulation

The following figures show different gaits of different profiles.

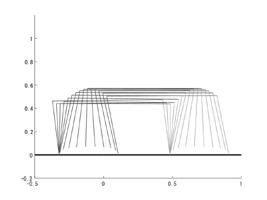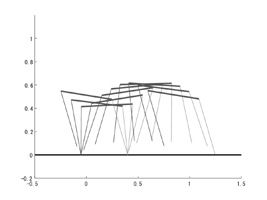Fig. 12 Passive quadruped bounding gait 1	Fig. 13 Passive quadruped bounding gait 2

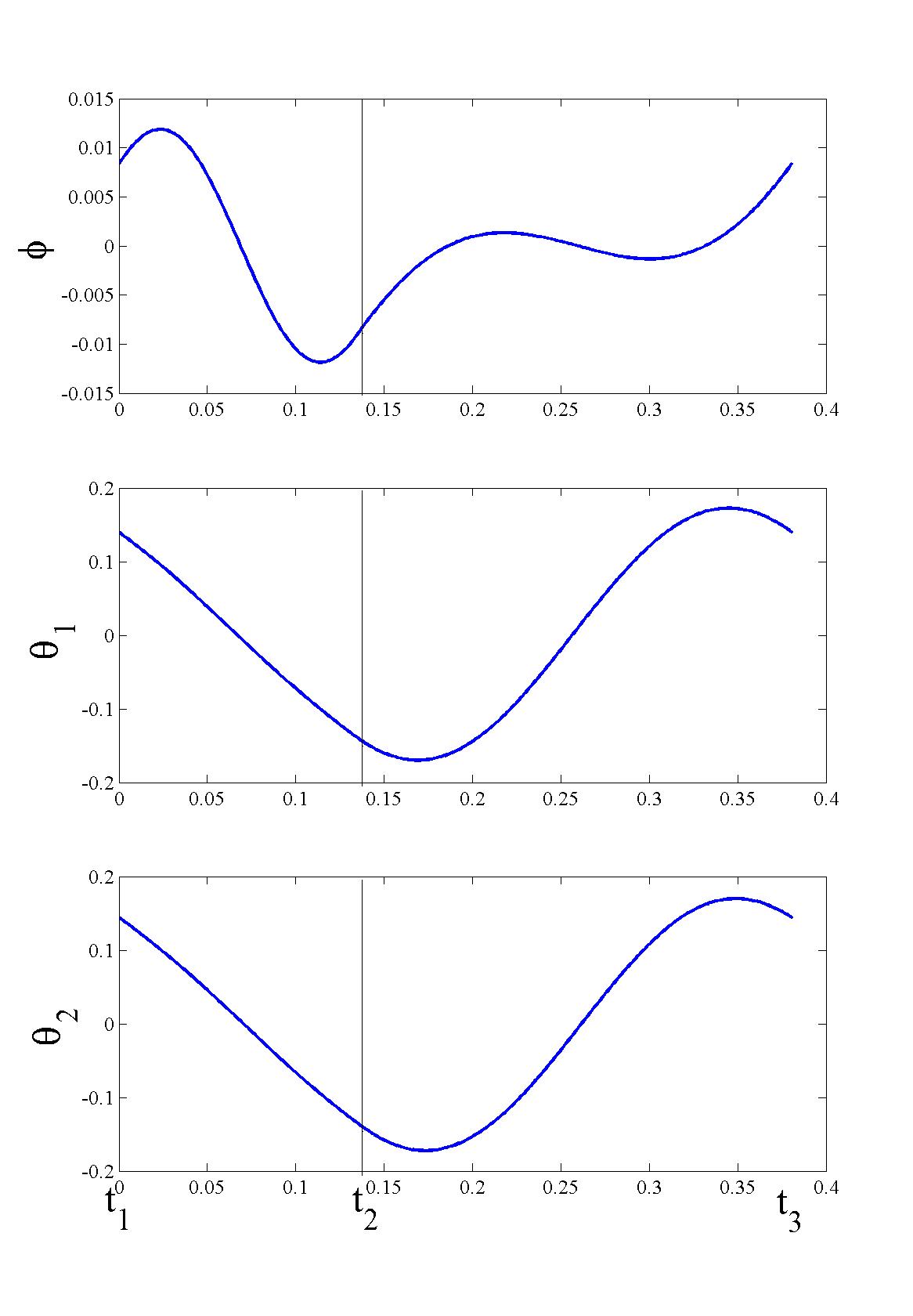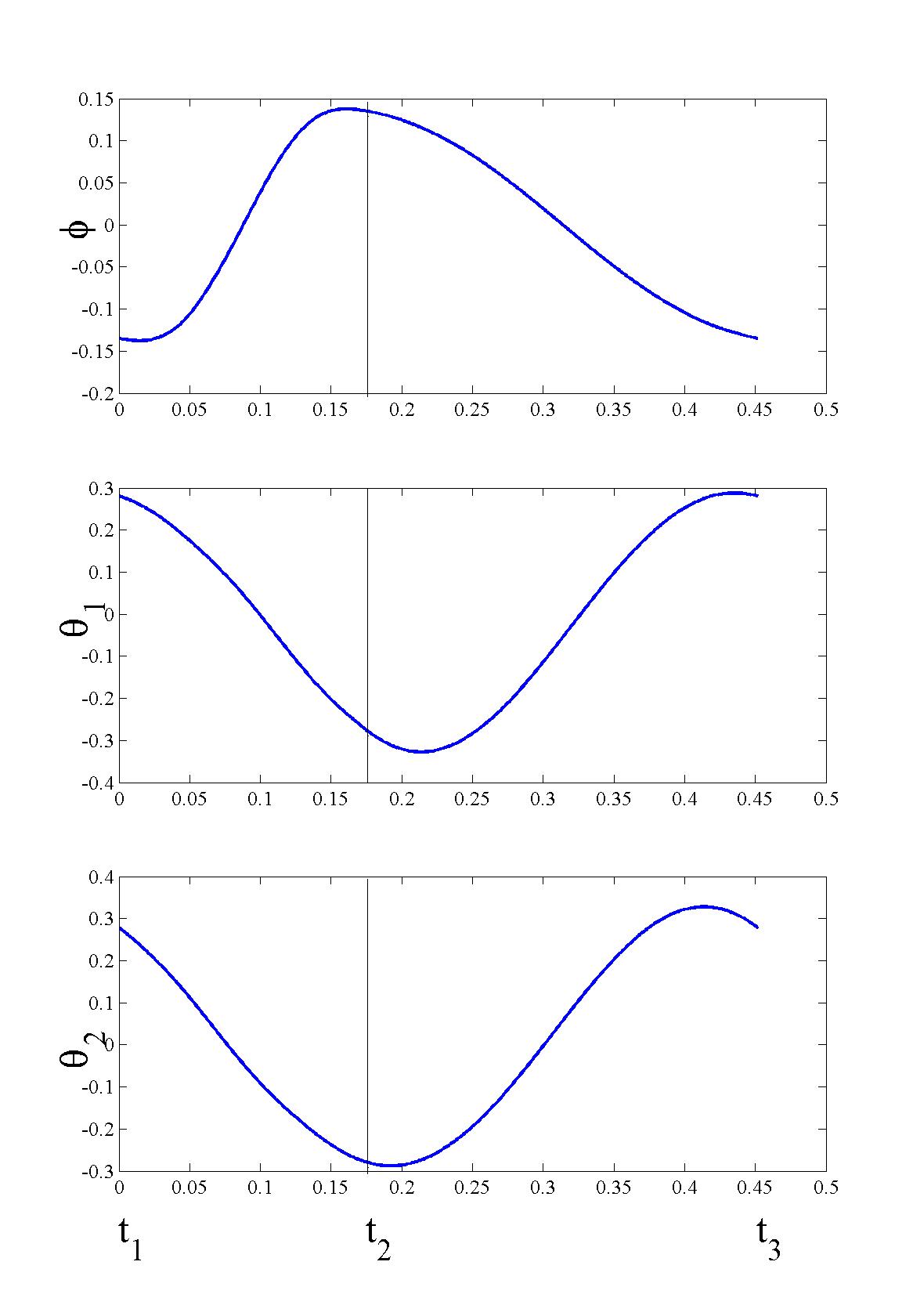Fig. 14 Passive quadruped bounding gait 1	Fig. 15 Passive quadruped bounding gait 2

Animation

• Passive quadruped bounding gait 1 [AVI 557K]

• Passive quadruped bounding gait 2 [AVI 3365K]

Another property we found from the passive running gaits is the symmetricity involved in the running pattern. Our simulations reveal that all the gaits of both Gait 1 and Gait 2 exhibit symmetrical behavior.

Our ongoing task is to develop orbital stabilization controllers.

4. Publication

• S. Satoh, K. Fujimoto and S. Hyon , "Gait Generation for Passive Running via Iterative Learning Control", in Proceedings of IEEE/RSJ International Conference on Intelligent Robots and Systems, Beijing, China, 2006.

• Satoh, S., Fujimoto, K. and Hyon, S., "Gait generation for a one legged hopping robot via iterative learning control based on variational symmetry", in Proceedings of IFAC Workshop on Lagrangian and Hamiltonian Methods for Nonlinear Control (LHMNLC06), pp.125-130, Nagoya, Japan, 2006.

• S. Hyon and T. Emura, Symmetric walking control: Invariance and global stability, IEEE International Conference on Robotics and Automation, pp.1455-1462, Barcelona, Spain, Apr. 2005.

• T. Ueta, T. Kousaka, T. Kawabe and S. Hyon, Partial external force control for piecewise smooth dynamical systems, The IASTED International Conference on Circuits, Signals, and Systems (CSS 2004), Florida, USA, 2004 (Accepted).

• S. Hyon, X. Jiang, T. Emura and T. Ueta, Passive running of planar 1/2/4-legged robots, Proc. of IEEE/RSJ IROS, Sendai, Japan, Sep 2004.

• S. Hyon, T. Emura and T. Ueta, Detection and stabilization of hybrid periodic orbits of passive running robots, Proc. of Mechatronics & Robotics, vol.4, pp.1309-1314, Aachen, Germany, Sept 2004.

• S. Hyon and T. Emura and T. Ueta, Delayed feedback control of one-legged passive running robot, Proc. of SICE Annual Conference, pp.949-954, Sapporo, Aug 2004.

• S. Hyon and T. Emura and T. Ueta, Nonlinear oscillations in legged running robots, IEICE NLP2004-9, pp.47-52, Sendai, Japan, May 2004 (in Japanese).

• S. Hyon and T. Emura, Running control of a planar biped robot based on energy-preserving strategy, Proc. of IEEE ICRA, pp.3791-3796, New Orleans, USA, Apr 2004.

• S. Hyon and T. Emura, Energy-preserving control of passive one-legged running robot, Advanced Robotics, vol. 18, no. 4, pp. 357-381, 2004.

• X.Jiang, S.Hyon, T.Emura , Gait analysis on a passive quardruped running robot, SICE Tohoku Chapter 213rd Workshop , 2003.

• S. Hyon and T. Emura, Aerial posture control for 3D biped running using compensator around yaw axis, Proc. of IEEE ICRA, 2003.

• T. Emura, S. Hyon and Y. Kuroda, A biped hopper controlled around yaw axis by body-twisting motion, Proc. of Int. Conf. on Mechatronics 2003 (ICOM2003), pp. 505-510, 2003.

• S. Hyon and T. Emura, Semi-passive running contorl for a biped robot with torso, Proc. of 45th SICE/JSME conference, 2002 (in Japanese).

• T. Emura, Y. Kuroda and S. Hyon, Development of telescopic 3D biped with compensator around yaw axis, Proc. of 45th SICE/JSME conference, 2002 (in Japanese).

• S. Hyon and T. Emura, Quasi-periodic gaits of passive one-legged hopper, Proc. of IEEE/RSJ IROS, pp. 2625-2630, 2002.

• S. Hyon and T. Emura, Toward passive running of biped robot, Proc. of 20th Annual Conference of RSJ, CD-ROM, 2002 (in Japanese).