歩行運動学習
研究目的
我々の研究室では、ヒューマノイドロボットを用いることを通じて、人間の運動生成および最適化の原理を明らかにすることを目指しています。人間の運動の最適化はこれまで2点間到達運動に関する研究が主に行われてきました。この2点間到達点運動は過渡的な運動ですが、その一方で人間の運動には歩行に代表されるような周期的な運動も多く現れます。そこで、我々は周期的運動に運動を特化した場合の運動最適化・学習モデルの構築を行いました。 具体的には、人間の歩行運動学習モデルを構築することを通じて、人間の歩行運動の理解と、さらには周期運動一般の最適化メカニズムを明らかにすることを目標とした歩行運動の最適化に関する研究を行ってきました。
我々の目標は、ヒューマノイドロボットでの歩行運動の実現そのものではなく、ヒューマノイドロボットでの歩行実現を通じて人間の歩行運動戦略を理解し、高齢者など歩行運動が困難な人を支援する手法を開発のための示唆を与えることにあります。ネコなどの動物では(神経)振動子が歩行の生成に重要な役割をはたしていることが知られています。そこで、人間の場合でも結合振動子系による同期メカニズムが周期運動の生成に関与しているという仮定の下に、振動子モデルを歩行生成に用いることを前提とした学習制御手法の研究を行ってきました。
強化学習法に基づく歩行の学習
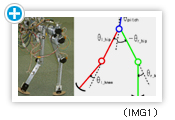
我々はまず、振動子モデルの適用手法を検討するために矢状面に拘束された、ヒューマノイドロボットに比べて単純化された歩行ロボットモデル(DB-chan)を用いたシミュレーションおよび実験(IMG1)を行いました。
初期検討で得られた知見に基づき、3次元の歩行ロボットモデル及びヒューマノイドロボットモデルへの拡張を行っています。ここでの問題は、初期検討を行った系に比べてヒューマノイドロボットは自由度が顕著に多いことです。一般に多自由度の系において、歩行運動のような非線形最適制御問題を解くことは困難です。特に、実環境における制御則の最適化は試行に必要とする時間やハードウェアの耐久性の問題からさらに困難な問題となります。しかし、人間の脳はそのような困難な問題に対して妥当な制御則を限られた回数の試行錯誤から導き出すことが可能なのです。
我々の研究においては、少ない実環境とのインタラクションからノンパラメトリックに環境のモデルを同定し、そのモデル上で制御則を最適化するアプローチを提案しました。これらのアプローチを、ヒューマノイドロボットを用いて評価を行ってきました。(動画右参照)
位相同期の学習
神経生理学等の実験により、四肢動物の基本的な歩行パターンは脳幹・脊髄によって生成され、そのリズムは小脳や脳幹を含む高次中枢や求心性入力によって調節されていることが示唆されています。この研究では適切な位相同期を行うために、方策勾配法による強化学習の枠組みを用いて脚接地時における位相制御方策を獲得する手法を提案し、その有効性を数値シミュレーションによって示しました。位相制御方策とは、位相Φの関数として位相制御量(シフト量)ΔΦ を与えるものです。
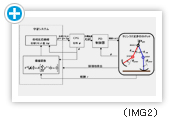
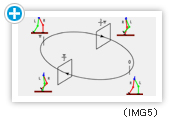
この研究で提案する学習システムでは、目的とする周期運動の達成度を報酬によって表現し、この報酬の累積値が最大となるよう位相制御方策を方策勾配法によって更新します。(IMG2)に提案する学習モデルを示しました。
歩行ロボットの各関節は、位相Φ に基づき周期的な関節目標軌道を出力します。位相制御方策は確率分布として表現し、接地時の位相Φ に応じて決定された位相制御量ΔΦ により位相を修正します。ここでは、(IMG1)に示す5リンクロボットモデルに対し提案手法を適用しました。
(IMG3)(上)に位相制御方策を用いない場合のシミュレーション結果を、(下)には学習により獲得した位相制御方策を用いたシミュレーション結果を示しています。学習により設計された位相制御方策を用いた場合は転倒していないことが分かります。
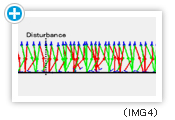
また、障害物が存在する路面上において、学習により獲得した位相制御方策を用いてシミュレーションを行ないました。障害物は足先が衝突する程度の高さに設定してます。また、衝突後に障害物が歩行を遮らないよう、衝突した脚が接地するかあるいは0.5秒以上時間が経過した場合に消滅するように設計しています。歩行パターンを(IMG4)に示しています。障害に躓いた後、位相を変位させることによって歩行を継続することができています。
Poincaré 写像に基づく局所歩行安定化制御器の学習
この研究では、2足歩行運動のための局所的な安定化制御器の学習を行いました。遊脚接地位置は、歩行ロボットの重心の運動を制御するための重要な変数となるため、ここではこの遊脚接地位置を制御出力としました。2足歩行運動の獲得に強化学習を適用した例があるが、この研究では、学習によって獲得されるPoincaréの写像と価値関数を用いて、効率的な歩行運動学習を実現します。
提案手法を評価するため、(IMG1)に示した5リンクのロボットモデル(DB-chan)を用いました。この2足歩行ロボットは胴体部が短く、足先が点接触および円弧接触であるため、2足歩行ロボットに広く用いられている、ZMPを基にした軌道計画および制御手法を適用することが困難です。この研究では、(IMG1)に示すような歩行ロボットモデルでも、歩行運動を獲得できることを示しています。
ここでは、モデルベース強化学習の枠組みを用います。強化学習に用いるモデルとして、Poincaréの写像を用いることにしました。また、この写像は学習を通じて獲得されます。価値関数の評価は歩行の半サイクル毎行われます(IMG5)。Poincaré切断面における現在のロボットの状態と、遊脚接地位置を決定する膝目標関節角から、半周期先のPoincaré切断面でのロボットの状態を予測します。たとえば、位相における状態から位相における状態を予測します。
遊脚接地時においては、床面との衝突により大きくロボットの状態が変化するため、ここでは単脚支持期におけるPoincaré切断面での状態を用いました。Poincaré写像の学習は、パラメータベクトルを持つ関数近似器によって実現されます。一周期の歩行軌道は、人間の歩行軌道をスケールしたものを経由点によって表現します。ここで、学習制御器はこの経由点の変更を歩行ロボットの状態に応じて行います。ここでは、それぞれの経由点を内挿する手法として、関節角躍度最小軌道を用いました。ロボットは継続して歩き続けることができれば、正の報酬、転倒すれば負の報酬を得ます。
強化学習の枠組みにおいては、累積報酬の期待値を最大化するような制御器の学習を行います。この研究で提案する枠組みでは、半周期毎に価値関数および制御方策の更新を行うためセミマルコフ決定過程での学習手法となります。
歩行制御器の学習は次のように行う。
1.1 現在の状態における価値関数の勾配を求める。
1.2 Poincare写像の勾配を求める。
1.3 価値関数の勾配とPoincare写像の勾配の内積によって、方策パラメータの変化による価値関数の勾配方向を求め、その勾配方向に方策パラメータを更新する。
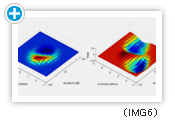
シミュレーションによって得られた結果を以下に示します。獲得された制御方策と価値関数を(IMG6)に示します。
同様にして、提案手法を(IMG1)に示した実ロボット(DB-chan)に適用しました。ビデオには学習前と学習後の歩行パターンを記録しています。(動画下参照)
参考文献
[1] Morimoto,J., Atkeson,C. G., Endo, G., & Cheng, G. Improving humanoid locomotive performance with learnt approximated dynamics via Gaussian processes for regression, In IEEE/RSJ International Conference on Intelligent Robots and Systems, pp. 4234-4240, San Diego, CA, USA (2007)