Goal

The goal of our study is to understand the principle of human motor control and optimal control strategies. Such discrete movements as two-point reaching arm movements have been studied to understand the optimal control strategy of humans. On the other hand, such periodic behaviors as biped walking have not been intensively studied from an optimal control viewpoint. We focused on optimization and learning algorithms for periodic movements, especially for the development of biped walking optimization algorithms to understand human biped control mechanisms.

To understand human biped walking strategies, we started to work on a central pattern generator model (CPG), which is a neural oscillator model of animals. The neural oscillator takes an important role for legged locomotion to synchronize the periodic patterns of body movements with environments. By assuming that humans are using CPG-based synchronization mechanisms, we developed learning algorithms for biped locomotion based on an oscillator model to generate periodic leg behaviors.

Reinforcement learning algorithms for biped locomotion

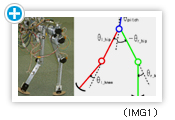
We first tested our CPG model on a simple biped robot named DB-chan that is constrained on a sagittal plane by a boom（see IMG1）.

We extended our idea of a CPG-based biped controller to a humanoid robot model. The humanoid robot model has many more numbers of degrees of freedom than DB-chan. In general, solving a non-linear optimal control problem is difficult for a system that has many degrees of freedom. The problem becomes especially complicated if we apply a policy optimization method to a real robot since many learning iterations are required to optimize the policies, and the hardware may be damaged during the learning trails. On the other hand, humans can learn proper control policies from a limited number of learning iterations.

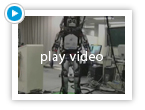
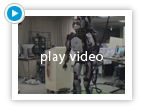
In our study, we identified environmental models using a non-parametric regression method from few learning iterations. Then we optimized the learning policies on the identified non-parametric model and tested our approach on humanoid robots（see the movie）.

Learning phase modulation policies

In this study, we proposed a learning algorithm of phase modulation policies based on a policy gradient method. The target of the policy is to synchronize the biped robot with its environments.

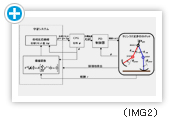
In our learning framework, each desired joint angle depends on the phase. The phase modulation policies are represented by probability distributions（see IMG2）.

The output of the phase modulation policies is the amount of phase modulation based on the current phase. We applied our proposed method to the simulated DB-chan model.

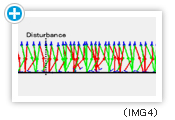
（see IMG3）(Top) Without phase modulation policies (Bottom) With an acquired phase modulation policy. The DB-chan model could walk without falling.

The DB-chan model could walk without falling even if its swing leg was disturbed by a simulated obstacle on the ground by an acquired phase modulation policy. The figure shows the generated walking pattern（see IMG4）. The DB-chan model could walk even after the presence of the disturbance by modulating phase based on the acquired policy.

Poincaré-map based reinforcement learning for learning biped locomotion

In this study, we propose to learn locally stable biped walking policies by estimating the Poincaré map through learning trials. We represent leg trajectories by a fifth order spline function that interpolates by points, which are modulated by an acquired walking policy.

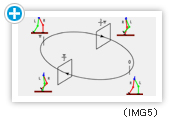
We optimize biped walking controllers based on an approximated Poincaré map using a model-based reinforcement learning framework. The Poincaré map represents the locus of the intersection of the biped trajectory with a hyperplane in the full state space.

In our case, we are interested in the system state at two symmetric phase angles of the walking gait. Modulating via points affects the locus of intersection, and our learned model reflects this effect（see IMG5）.

Since the policy output is only changed at the Poincaré section, our method can be considered a learning scheme for a policy to output a proper “option” for a Semi-Markov Decision Process (SMDP).

We derive the update rule for a policy using the value function and the estimated Poincaré map.

The update rule is the following:

1.1 Derive the gradient of the learned Poincaré map model.

1.2 Derive the gradient of the approximated value function.

1.3 To update the policy parameter, compute a desired output by the inner product of the gradients of the value function and the Poincaré map.

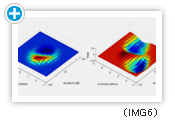
　Acquired value function and policy are presented in （IMG6）.

We applied the proposed learning method to the real biped robot(DB-chan). Movies show walking behaviors before and after the learning process.(See below)

References

[1]　Morimoto，J.， Atkeson，C. G.， Endo， G.， & Cheng， G. Improving humanoid locomotive performance with learnt approximated dynamics via Gaussian processes for regression， In IEEE/RSJ International Conference on Intelligent Robots and Systems， pp. 4234-4240， San Diego， CA， USA (2007)